Amplitude

The amplitude Ê is a measure for the intensity (brightness) of light. For from a graphical point of view the amplitude describes the height of a wave crest, respectively the depth of a wave valley, measured from an imaginary horizontal line running right through a sinusoidal curve, light with a large amplitude is bright light, while darker light has got smaller amplitude.

"Die Amplitude einer Schreibtischlampe ist größer als die einer Streichholzflamme, die Amplitude des Sonnenlichts wiederum größer als diese beiden.

Mit der Entfernung ändert sich die Amplitude des Lichts. Nahe bei seiner Quelle ist das Lichts stärker und wird immer schwächer, je weiter es sich davon entfernt. Das erklärt sich durch die Tatsache, daß sich Licht auf seiner Reise ausbreitet. Die Energie einer ganzen Wellenfront bleibt zwar gleich, aber die Intensität wird geringer, da die Front eine größere Fläche abdeckt. Sind wir z. B. doppelt so weit von der Lichtquelle entfernt, als vorher, beträgt die Intensität nur noch ein Viertel."

[The amplitude of a desk lamp ist larger than the amplitude of a match's flame. The amplitude of sunlight is larger than both of them.

The amplitude of light changes with the distance. Close to its source light is stronger and gets weaker the farther it removes. This circumstance is explained by the fact that light propagates on its journey. The energy of all of a wave front remains the same, but the intensity gets smaller, for the front covers a larger area. For light departs twice the distance from its source, its intensity amounts just a quarter.]

Referred to the graphical illustration of the sinusoidal curve this means: "[...] if one wave has twice the amplitude of another, the first light has four times the intensity of the second."

"Das ist das Gesetz vom inversen Abstandsquadrat, welches besagt, daß die Lichtintensität umgekehrt proportional zum Quadrat der Entfernung abnimmt. Bei dreifacher Distanz beträgt die Intensität also nur noch ein Neuntel."

[This is the law of inverse square of the distance, which says, that light intensity declines inverse proportional to the square of the distance.]

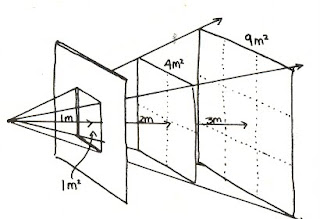
Fig. Law of inverse proportional light intensity

The following figure would like to illustrate the above described:

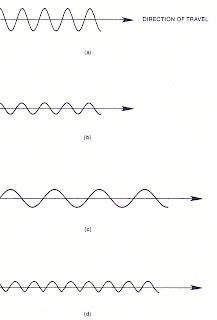
Fig. Intensities of different light waves

The waves in (a) and (b) have got the same wave length, but the light in (a) is more intense (brighter) than in (b) - (a) has got a larger amplitude than (b). The ratio between these to waves is about 2:1. Therefore light (a) is four times (2²) brighter than light (b). (c) has got he same intensity as (b), but a larger wave length. (d) again has got the same intensity as (b), but a shorter wave length.

The sinusoidal is therefore a graphical illustration of intensity variation of the energy of light, that travels as a particle photon wave-like through space and time.

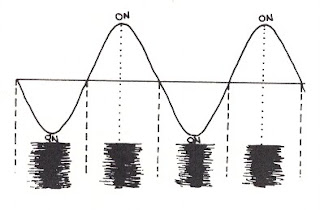
Fig. Light photon passes two cycles

It passes a whole cycle, starting at »off« (zero point), passing »on« (wave crest), back to »off« (zero point), passing »on« (wave valley), and back to »off« (zero point).